Introduction
fig. 1 picture from 'Multiview geometry in Computer Vision' book.
If you use orthogonal regression ( minimizes the sum of squared perpendicular distances -- LMS ), there will be a problem if you have an outliers (see fig 1a).
RANSAC algorithm
- First we randomly pick two red point and estimate m, c for y=mx+c ( this is easy, right )
- for consider if a point is a inlier
for every yellow point (x, y)
If | y - (m*x + c) | < t, number of inlier need to justify model
-- re-estimate m, c again by using all the inlier
a simple python example code for RANSAC is available here.
or more complicate code here. all is the same code as a psudocode from wiki.
or you can use my porting octave code here ( NOTE if you are using matlab, this code should be modified )
adaptively find k (the number of iterations)
k = log(1-p)/log(1-(1-ε)^n)
p = prob(RANSAC algorithm in some iteration selects only inliers )
w = prob( choosing an inlier each time a single point is selected ) = number of inliers / number of all points
A common case is that w is not well known beforehand, but some rough value can be given.
n = Sample Size
wn = prob( n points are inliers )
1 − wn = prob( at least one of the n points is an outlier ) [ bad model will be estimated from this point set ]
( 1 − wn k = prob( algorithm never selects a set of n points which all are inliers )
( 1 − wn )k = 1 − p
take log and we will get
k = log(1-p)/log(1-w^n)
It should be noted that this result assumes that the n data points are selected independently, that is, a point which has been selected once is replaced and can be selected again in the same iteration.
Apply to Homography
When adapt this to Homography, estimating line is not a visual line. The error is computing from transfer error d.
This RANSAC for Homography steps are adapt from Alexei (Alyosha) Efros's slide.
RANSAC loop:
1. Select 4 feature pairs (at random)
[ n in the code, or s in the book is fixed to 4 ]
2. Compute homography H (exact)
3. If d(x’, H x) largest set of inliers
[ so the number of inliers needed to justify the model ( d in the code or capital T in the book ) is not used here. ]
5. Re-compute least-squares H estimate on all of the inliers
fig. 1 picture from 'Multiview geometry in Computer Vision' book.If you use orthogonal regression ( minimizes the sum of squared perpendicular distances -- LMS ), there will be a problem if you have an outliers (see fig 1a).
RANSAC algorithm
RANSAC algorithm will cope with this problem by discarding outliers.
Slide from 25th year of RANSAC, Philip Torr slides has very clear picture of the algorithm.
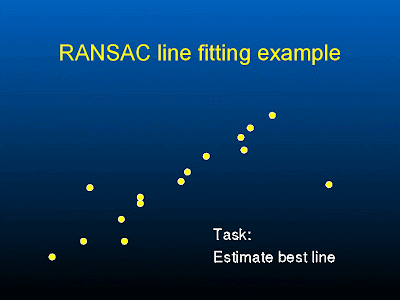
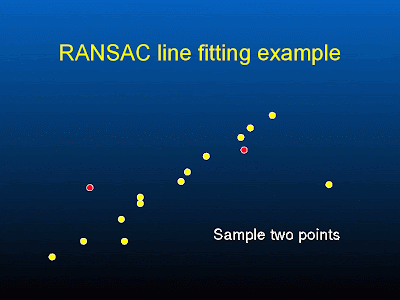
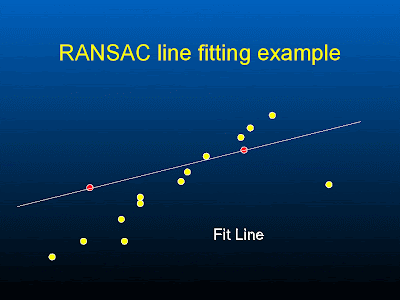
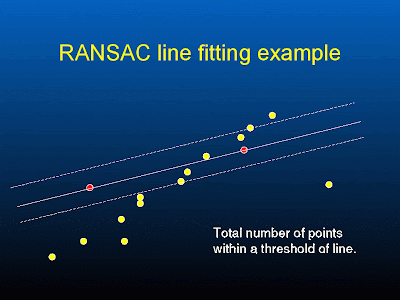
support = number of points that lie within a distance threshold
points within the threshold distance of a line with most support are the inliers.
If a point is an outliers, a line will not have so much support. ( see fig 1b from mvg book above )
Explain the algorithm
Slide from 25th year of RANSAC, Philip Torr slides has very clear picture of the algorithm.
support = number of points that lie within a distance threshold
points within the threshold distance of a line with most support are the inliers.
If a point is an outliers, a line will not have so much support. ( see fig 1b from mvg book above )
Explain the algorithm
- First we randomly pick two red point and estimate m, c for y=mx+c ( this is easy, right )
- for consider if a point is a inlier
for every yellow point (x, y)
If | y - (m*x + c) | < t, number of inlier need to justify model
-- re-estimate m, c again by using all the inlier
sample code ?
a simple python example code for RANSAC is available here.
or more complicate code here. all is the same code as a psudocode from wiki.
or you can use my porting octave code here ( NOTE if you are using matlab, this code should be modified )
# Run RANSAC to see if we can recover the line (y=x) from the data.
function [model_params, model_error, model_inliers] = ransac(data,n,k,t,d)
% k -- the number of iterations.
% t -- the threshold for deciding when a data point fits a model (i.e. is an inlier).
% d -- the number of inliers needed to justify the model.
# k=100,d=20
model_params = [0.0, 0.0] # slope and intercept
model_error = 1e6
model_inliers = []
for i=1:k # k iterations
fprintf(1, "new iteraion\n\n")
inliers = choice(data, n)
# Fit a line (or generally any model) using lstsq.
a = [inliers(:,1), ones(1, n)']
b = inliers(:,2)
# linear least square -- rewrite y = mx+c in y = A*p form
# A = [x 1]
# p = [m, c]
p = a \ b
compatible = []
for j=1:size(data, 1)
fprintf(1, '--')
pt = data(j,:)
if abs(pt(2) - dot(p, [pt(1), 1.0])) < t # | y - (m*x + c) | < t
compatible = [compatible; pt]
end
end
if size(compatible, 1) > d
# The current model is good enough so we should recompute it using all compatible points.
a = [compatible(:,1), ones(1, size(compatible, 1))']
b = compatible(:,2)
p = a \ b
# if residuals < model_error
model_params = p
# model_error = residuals
model_inliers = compatible
# end
end
end
function result=choice(seq, n)
indx = 1:size(seq)-1
shuffle(indx)
result = seq(indx(1:n), :)
adaptively find k (the number of iterations)
k = log(1-p)/log(1-(1-ε)^n)
p = prob(RANSAC algorithm in some iteration selects only inliers )
w = prob( choosing an inlier each time a single point is selected ) = number of inliers / number of all points
A common case is that w is not well known beforehand, but some rough value can be given.
n = Sample Size
wn = prob( n points are inliers )
1 − wn = prob( at least one of the n points is an outlier ) [ bad model will be estimated from this point set ]
( 1 − wn k = prob( algorithm never selects a set of n points which all are inliers )
( 1 − wn )k = 1 − p
take log and we will get
k = log(1-p)/log(1-w^n)
It should be noted that this result assumes that the n data points are selected independently, that is, a point which has been selected once is replaced and can be selected again in the same iteration.
Apply to Homography
When adapt this to Homography, estimating line is not a visual line. The error is computing from transfer error d.
This RANSAC for Homography steps are adapt from Alexei (Alyosha) Efros's slide.
RANSAC loop:
1. Select 4 feature pairs (at random)
[ n in the code, or s in the book is fixed to 4 ]
2. Compute homography H (exact)
3. If d(x’, H x) largest set of inliers
[ so the number of inliers needed to justify the model ( d in the code or capital T in the book ) is not used here. ]
5. Re-compute least-squares H estimate on all of the inliers
ความคิดเห็น